Storing Graphs

There are multiple ways of storing graphs. Depending on the type of graph and the requirements a certain storage method might be preferred.

Adjacency matrix

An adjacency matrix is a matrix that is $n \times n$, with $n$ being the number of vertices in the graph. As the name suggests this matrix stores the adjacency of vertices i.e the relationship between vertices (edges).

For a weighted graph we have the matrix int[][] G = new int[n][n] where the value stored at G[x][y] corresponds to the weight of the edge from vertex $x$ (row) to vertex $y$ (col). If there is no edge between 2 vertices then there are multiple ways of conveying this. Either the value is set to 0 or Integer.MAX_VALUE or we use an object array (Double or Integer) and set the value to null.

If the graph is unweighted we can either use the same 2D int array and just store all edge weights as 1 or use a 2D boolean array which interestingly does use less space in java. In Java a normal boolean variable uses 32 bits like an int however in an array each boolean value only takes up 8 bits. 8 bits because that is what the CPU likes to work with, it doesn't like reading/writing a single bit.

If the graph is undirected then mathematically $G = G^T$ which means if there is an edge between the vertices $x$ and $y$ the value needs to be set at [x][y] and [y][x].

The biggest problem with storing graphs with an adjacency matrix is that $O(n^2)$ memory is used and a lot of the space is wasted as in most cases there are only a few edges between vertices and we don't need to be able to store every possible combination.

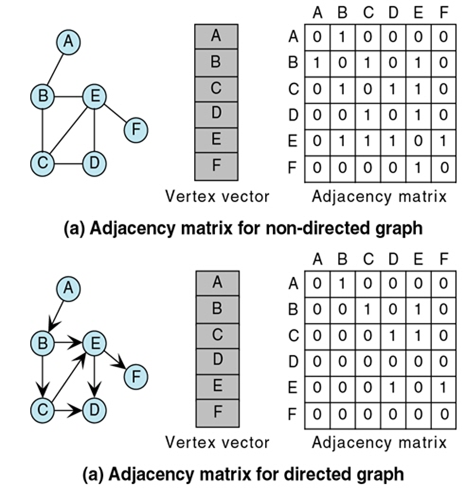
Adjacency matrices are however very easy to implement:

public class UndirectedUnweightedGraph {
    private final boolean[][] adjMatrix;
    public final int n;

    public GraphI(int numNodes) {
        if (numNodes < 1) throw new IllegalArgumentException();
        this.adjMatrix = new boolean[numNodes][numNodes];
        this.n = numNodes;
    }

    public boolean addEdge(int u, int v) {
        if (0 <= u && u < n && 0 <= v && v < n) {
            if (adjMatrix[u][v]) return false; // already set
            adjMatrix[u][v] = adjMatrix[v][u] = true;
            return true;
        }
        throw new IndexOutOfBoundsException();
    }
}

Edge table

Another easy but less common way of storing graphs is just storing a list of the edges. The edges could have the following structure:

class Edge {
 int from, to, weight;
}

If it is an unweighted graph the weight attribute could just be omitted and if it is an undirected graph you can either have two entries for each edge or handle from and to the same way depending on your implementation.

The advantage of this solution is that it only uses $O(m)$ memory with $m=$ the number of edges. The disadvantage of this storage solution is that you can not quickly find out how many or what vertices are in the graph. This could however be resolved by just adding another list containing all the vertices. This solution would then be very similar to the mathematical description of a graph where $G=(V, E)$ and $V$ is the set of vertices and $E$ is the set containing pairs of vertices for the edges. This would then have a memory usage of $O(n+m)$ with $n$ being the number of vertices and $m$ the number of edges.

Adjacency list

An adjacency list is very similar to an edge table. Each vertex has an adjacency list of all the edges it has. To then store the entire graph we have a list of adjacency lists. An adjacency list can just be a simple array but it is a linked list due to the storage and length being dynamic. If the graph is undirected you can again either handle it by just storing it in one adjacency list or both adjacency lists. This structure uses just like the edge table $O(n+m)$ memory with $n$ being the number of vertices and $m$ the number of edges.

public class UnweightedGraph<K> {
    private static class Vertex<K> {
        K data;
        int indegree, deg = 0;
        boolean visited;
        List<Vertex<K>> adjList = new LinkedList<Vertex<K>>();

        Vertex(K value) {
            data = value;
        }

        boolean addEdgeTo(Vertex <K> to) {
            return (adjList.contains(to)) ? false : adjList.add(to);
        }
    }
    
    private Map<K, Vertex<K>> vertices;
    private int nOfEdges = 0;

    public UnweightedGraph() {
        this(false);
    }

    public UnweightedGraph(boolean directed) {
        super(directed);
        vertices = new HashMap<K, Vertex<K>>();
    }

    public UnweightedGraph(UnweightedGraph<K> orig) { // copy constructor
        this(orig.isDirected());
        for (K k: orig.vertices.keySet()) {
            addVertex(k);
        }
        for (Vertex<K> v: orig.vertices.values()) {
            for (Vertex<K> w: v.adjList) {
                addEdge(v.data, w.data);
            }
        }
    }

    public boolean addVertex(K vertex) {
        if (vertex != null && !vertices.containsKey(vertex)) {
            vertices.put(vertex, new Vertex<K>(vertex));
            return true;
        } else {
            return false;
        }
    }

    public boolean addEdge(K from, K to) {
        Vertex<K> vf = vertices.get(from);
        Vertex<K> vt = vertices.get(to);
        if (vf != null && vt != null && vf.addEdgeTo(vt)) {
            vt.indegree++;
            if (!isDirected()) {
                vt.addEdgeTo(vf);
                vf.indegree++;
            }
            nOfEdges++;
            return true;
        } else {
            return false;
        }
    }
}